8 幾何図法におけるパソコンの利用

最近は種々の職場にパソコンが浸透してきたので、現図場におけるパソコンの簡単な利用法について触れる。

現図場において、例えば大きな円弧を描く際に作図スペースの確保に苦労する場合、幾何図法による手順が複雑でもっと簡単に描きたい場合、或は近似的でなくより正確な図形を描きたいというような場合がある。

このような場合には、コンパス等を用いた幾何図法によらず、作図点を数値計算による座標値として得る方が便利である。即ち、アナログ的な手法をパソコンを利用してディジタル的な手法に変える方法である。

本章においては、パソコンを利用した数値計算により、作図用の座標値を算出する方法について、その一例を紹介する。

なお、本章で述べる内容は、パソコンに限らずプログラム電卓やポケットコンピュータを利用しても、ほぼ同様のことができる。

8.1 任意の3点を通る円又は円弧

任意の3点A,B,Cが形成する三角形ABCにおいて各辺の長さをl,m,nとする。1辺の長さが最も長いABをx軸とし、ABの垂直2等分線をy軸とすれば、3点A,B,Cを通る円は

ここにyO：円の中心Oのy座標の値

R：円の半径

円OはB（l/2,0）を通るから

C点の座標をC（a,h）とすれば

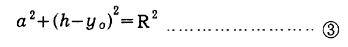
?A、?B式よりRを消去すれば

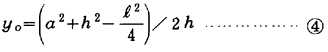
三角形ACD及びBCDにおいて

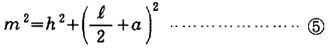
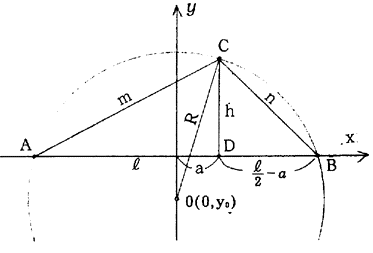
図1.35

前ページ　　　目次へ　　　次ページ